Binary Coded Decimal
The Binary Coded Decimal (BCD) number system is used to represent decimal numbers (0 to 9) using four-bit binary codes. We also refer to it as the BCD number system.
For example, the binary conversion of the decimal number 7 is (111)2, but in the BCD system, it is represented as (0111) in its four-bit form. Similarly, the numbers from 0 to 9 are represented in the same way as in the binary system. However, after 9, the representation in BCD is different. For instance, the decimal number 12 in binary is (1100)2, but in BCD, it is represented as [0001 0010], where each digit (1 & 2 separately) is replaced by its equivalent 4-bit binary form.
The table below shows the representation of decimal numbers from 0 to 15 in both binary and equivalent BCD form:
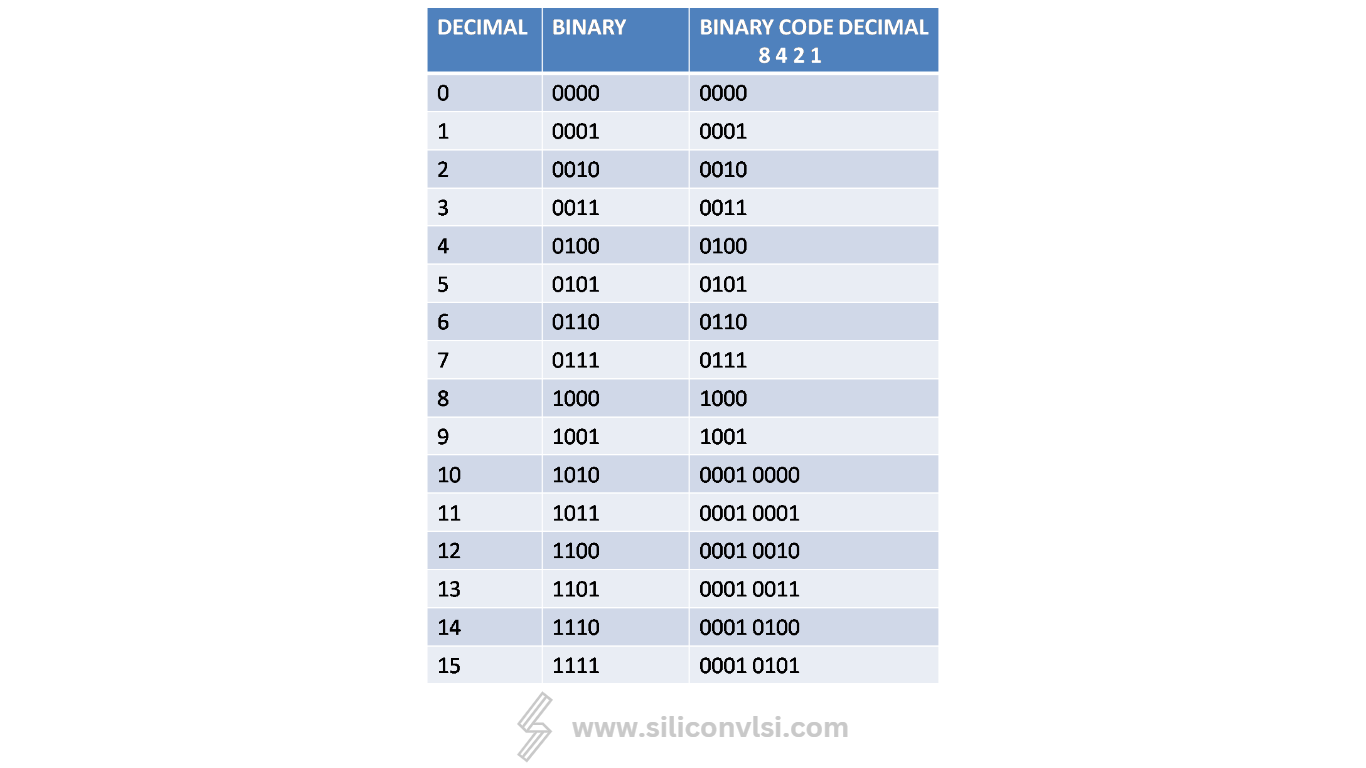
| Decimal Number | Binary Number | Binary Coded Decimal (BCD) |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0010 |
| 3 | 0011 | 0011 |
| 4 | 0100 | 0100 |
| 5 | 0101 | 0101 |
| 6 | 0110 | 0110 |
| 7 | 0111 | 0111 |
| 8 | 1000 | 1000 |
| 9 | 1001 | 1001 |
| 10 | 1010 | 0001 0000 |
| 11 | 1011 | 0001 0001 |
| 12 | 1100 | 0001 0010 |
| 13 | 1101 | 0001 0011 |
| 14 | 1110 | 0001 0100 |
| 15 | 1111 | 0001 0101 |
To convert a decimal number into its equivalent BCD form, each digit of the decimal number should be replaced by its equivalent four-bit binary form. For example, to get the BCD equivalent of the decimal number 874, replace each digit (8, 7, and 4) with its four-bit binary form (1000, 0111, and 0100). Then, combine these binary forms to get the BCD form, which is [1000 0111 0100]. Similarly, you can perform BCD addition using specific rules.
Advantages and Applications of Binary-Coded Decimal (BCD)
Size Limitations: Binary-coded decimal (BCD) system provides a solution to overcome the size limitations imposed on integer arithmetic. It allows the representation of decimal numbers using four-bit binary digits, which is convenient for handling and storing numeric data.
Human-Readable Numerals: BCD enables easy conversion between machine-readable and human-readable numerals. This feature is beneficial in applications where data needs to be presented in a human-friendly format.
Easy Coding and Decoding: Compared to the standard binary system, coding and decoding of BCD numbers are straightforward. BCD numbers can be easily converted to their equivalent decimal representation and vice versa, making it efficient for arithmetic operations involving decimal values.
Fast and Efficient Conversion: BCD offers a fast and efficient system for converting decimal numbers into binary numbers. This is particularly useful in applications that require frequent conversions between decimal and binary representations.
Limitations of Binary-Coded Decimal (BCD)
Increased Storage Requirements: Representing decimal numbers in BCD format requires extra bits of storage in a computer’s memory. This can lead to inefficiency in memory usage when compared to pure binary representations.
Circuit Complexity: BCD requires increased circuit complexity compared to the standard binary system. This complexity can have implications for the design and manufacturing of integrated circuits.
Wasteful Representation: BCD can be wasteful in terms of the number of states used. Many 4-bit states (10 to 16) in BCD are not utilized, which leads to inefficient utilization of binary digits.